In this article, we're going to talk about the incremental internal rate of return. so the reason we need an incremental in IRR is that let's say we had a situation where we had a cost of capital of 8% and we have 2 different projects or 3 projects and we say oh look the return on "Project 1" is 21% the return on another is 28% and then the return on another is 30%. We can't just say oh well let's just look and pick the highest IRR and say oh that's the project we want to do and the reason that we just can't look at one IRR and compare to another is that projects are going to differ based on the scale of the investment the timing of the cash flows in the riskiness of those cash flows.
So when we're trying to compare projects based on IRR we can run into problems when we have differences that quote on these three levels. Incremental IRR is basically finding a way for us to compare two projects based using the IRR method. So let's walk through an example it's a little bit obtuse but I think once we walk through it'll be easier for you to understand.
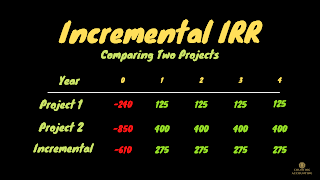
Let's say we've got two projects that we're trying to choose between. Now the cost of capital for both projects is 10% so whatever project we're talking about the cost of capital is 10%. Now we've got "Project 1" and "Project 2" our cash flows will take place over four years.
Year zero is just our initial upfront investment here and that's going to be negative in each case. We've got a negative investment followed by positive cash flows. So for project 1 negative -240, we put out upfront and then we get $125 a year for the next four years. In project 2 we lay out -850 upfront as an investment and get $400 for each of the next four years.
Now we can use an Excel function equals IRR and then just put in the cells here and thats will give us the internal rate of return,
If you want to calculate it by hand that's up to you but I've already calculated it and so for project 1 the IRR would be 38% and for project 2 the IRR would be 31% I'm just I've rounded these numbers here Now again you might say "Hey look we've got a bigger number right here so the decision is easy to go with the one that has a higher rate of return but remember we just talked about how there are differences in scale of the investment then that can actually lead us to a different decision.
So look at the differences here in terms of scale project two we're actually outlaying a lot more money but then we're getting a higher amount of cash flow each year so even though it has a different lower IRR we should still go ahead and compute the incremental IRR. The way we calculate this incremental IRR is we're looking at one project versus the other.
So let's take project 2 and say what are the incremental cash flows of project two versus project one. so upfront we're paying eight $850 as an investment versus paying $240. so one way to think about that is we're actually paying an extra -$610 and that's negative -$610 because we're investing this money.
This is a cash outflow it's an additional negative -$610 for us to do project 2 versus project 1. The way I get that is the difference between 850 and 240 is 610. So now when we think about the positive cash flows going forward each period we're going to have a positive 275, so what does that mean? That means that project 2 in each of the next 4 years is going to have an additional $275 positive cash flow each year. How did I get that number? 400 minus 125 dollars, now you might say well why didn't we take 125 and minus 400? Well because we're looking at from the advantage point of the project 2 incremental to project 1. Project 1 is like the baseline so to speak, and we're saying how much more cashflow do we have when we do project 2.
So the incremental cash flows are the difference or we can say we're looking at the margin here cash flows of project 2 verse project 1 this is what the cash flow is going to look like negative -610 upfront and then positive $275 for each of the next four years. now we can take this string of cash flows and we can compute in IRR for that string of cash flows. I've already done that, again I just use the IRR function in Excel and it comes out to 29%.
Now how do we interpret this 29%? The way we interpret is we take this 29% and we compare it to our cost of capital which is 10% remember we said it's the same for each project? We compare the incremental the 29% and say is that higher than 10%? Yes, it is, well what does that mean? That means it is profitable for us to switch from project 1 to project 2.
In other words, if we had project 1 and we were saying wait what if we did project 2 what would be the incremental cash flows, and would it be more profitable for our firm to switch to project 2? The answer is yes because the incremental internal rate of return exceeds our cost of capital. Now bear in mind the reason for this is that the scale of this project. The scale is a lot larger than project 1 so we have another article where we talk about how we can compare IRR based on two different projects and so forth so I'm not going to get into that but I do want to mention a really important caveat, actually several caveats that I'm going to have here.
So one is that if all the negative cash flows do not proceed or occur before the positive cash flows so just take a look at the cash flows so we've got negative cash flow followed by positive cash flows for the incremental IRR.
If that's not the case let's say we add a negative one thrown in the middle then we might not have an IRR or we might have multiple internal rates of return. We might have all those kind of problems that we talked about issues that we can run into with IRR when we don't have where the negative cash flow comes first followed by the positive cash flows even if that was the case for all the cash flows for the projects on a standalone basis even if that was fine if we have that violated for the window incremental cash flows we can have all kinds issues and then in that case obviously you just need to use net present value
Now here's something else that's very important the incremental IRR. This is telling us whether it's profitable to switch from project 1 to project 2 where project two is more profitable but it's not telling us on a standalone basis we talked about standalone. If we just looked at project 1 we just looked at project 2 if the NPV is positive, we don't know that and you could talk about "Well we can compute the NPV or we can look at the IRR this individual" you can talk about different things but just because we have an incremental IRR that exceeds our cost of capital does not mean necessarily be either the project's on its own has a positive NPV and should be accepted.
So if really this incremental IRR is this long as to compare and see if one project better than the other in terms of you know relative to one another is one more profitable than the other. Now here's our issue which you and this is got this kind of maybe a little obvious you might as fathers already, we assumed that the cost of capital 10% was the same for each project but as you know sometimes different projects we have a different opportunity cost of capital so what if for example, we had cost to capital for one project was 10% and then the other project was 19% well in this case we had a 29% incremental rate of return, so it doesn't matter but what if our incremental IRR was 15% and then we have these two different projects here well one has 10% and one has 19% is the cost capital. Which one do we compare this to? If we compare it to the 10% that says oh this is good if we compared to the 19% it doesn't look so good so when we have different costs of capital for the different projects that can kind of make our incremental IRR comparison go haywire and in that case you just want to go with the old reliable net present value because NPV will always give you the right decision in terms of choosing projects.